I'm a Computer Science PhD candidate in the Computer Animation group at RWTH Aachen University.
My research is focused on methods for simulating deformable solids for computer graphics,
though I'm both passionate about and have experience with simulating a variety of physical phenomena.
My broader interests encompass a variety of disciplines across mathematics, physics and computer science.
Simulation
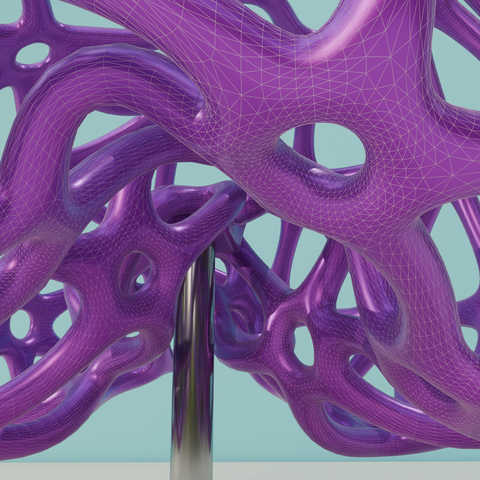I have a keen interest in physics simulation, with a penchant for the macroscopic — the things visible to the naked eye.
I have a background in numerics, including training in the mathematics of the Finite Element Method (FEM),
which I've carried over to my doctoral studies in physically-based animation,
a branch of Computer Graphics that focuses on the realistic reproduction of physical phenomena.
This path has allowed me to work on a number of interesting problems, including soft and rigid body mechanics,
real-time game physics and several approaches to fluid simulation.
Besides my research on simulation algorithms, I have designed and been teaching the Game Physics course
at RWTH Aachen University for several years.
Software
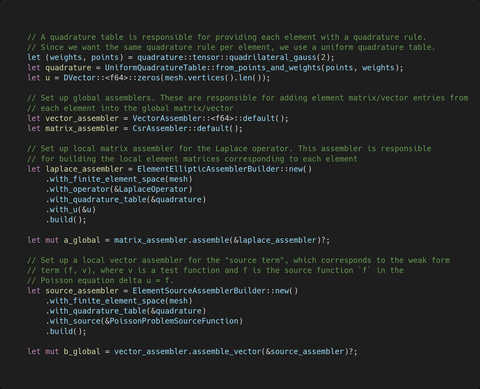In the two decades since my first foray into coding, I have touched upon many subfields of software development.
My combined passion for simulation and math has taken me down the path of scientific computing.
I have education in and professional experience with High Performance Computing (HPC).
I am passionate about writing performant, robust and above all correct code.
While proficient in a number of programming languages, I have developed an interest in Rust.
Since 2016, I have been contributing to its scientific ecosystem. Among other things, I am a co-maintainer of the nalgebra linear algebra library,
and I was a co-organizer of the first Scientific Computing in Rust workshop in 2023.
I also develop fenris, an experimental Finite Element library
that I use in my research.
Mathematics
I have an educational background in applied mathematics, with an emphasis on numerical analysis.
I have extensive experience with numerical linear algebra, solvers for partial and ordinary differential equations, and optimization theory and algorithms.
In recent years I've also been getting increasingly involved with computational geometry.
I enjoy modeling problems mathematically, thinking deeply about their mathematical structure,
and bringing the resulting equations to life through simulation and visualization.
